ASSONOMETRIE.

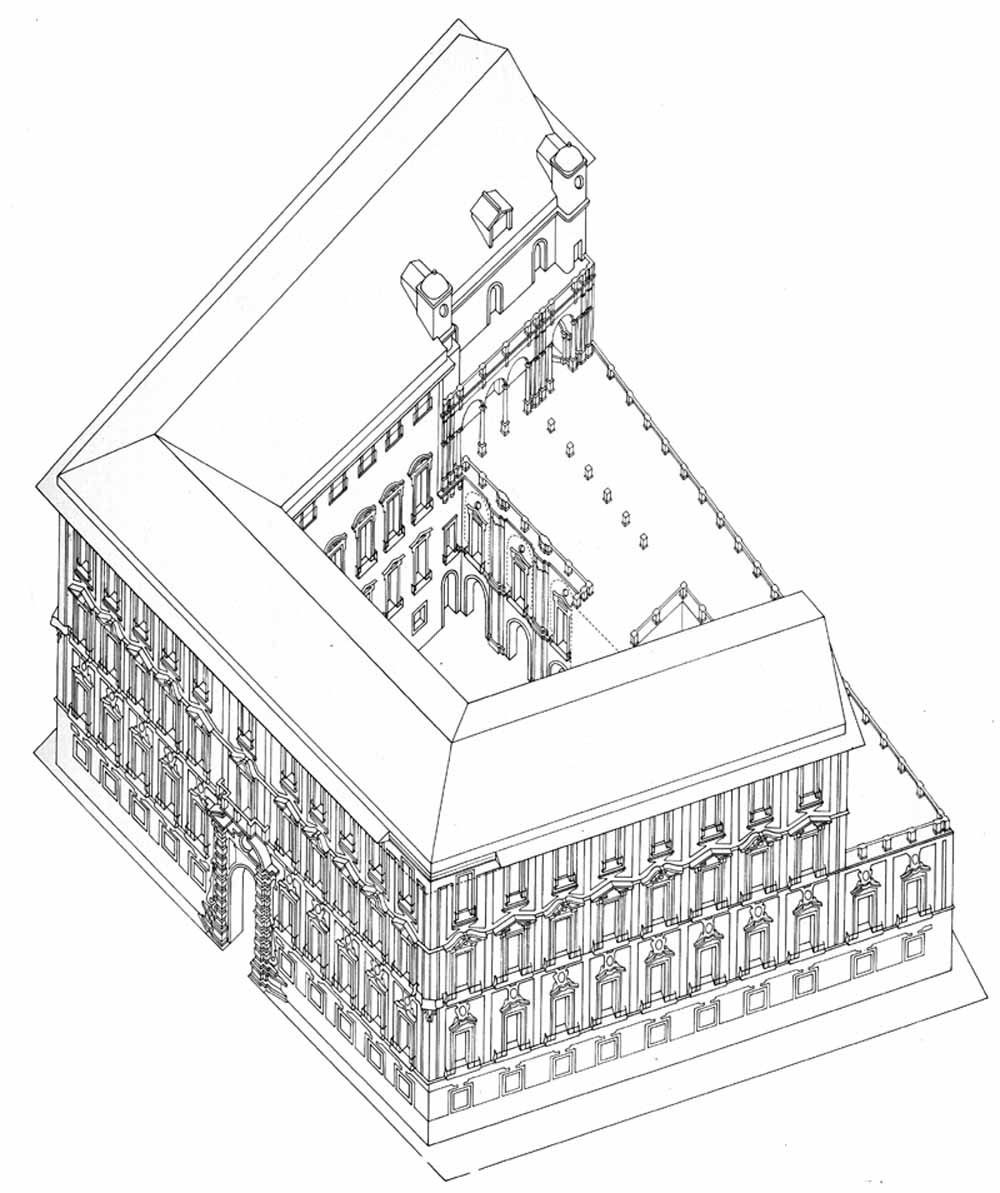
L'assonometria (o prospettiva assonometrica) si basa sul presupposto che l'osservatore sia collocato all'infinito in modo che i raggi visuali provenienti dal suo occhio (punto di vista) siano tutti paralleli fra loro. Gli elementi fondamentali della rappresentazione assonometrica sono:
-gli assi cartesiani x, y, z (ortogonali fra loro), uscenti da un'origine O, derivanti dall'intersezione di tre piani a1 a2, a3 fra loro perpendicolari. Essi rappresentano la direzione della larghezza (x), della profondità (y) e dell'altezza (z); l'asse z è sempre verticale.
-iI quadro assonometrico (II) è il piano sul quale si proiettano i tre assi x, y, z e dove si forma l'immagine assonometrica. Esso corrisponde al foglio da disegno e può essere parallelo o inclinato rispetto ai tre assi. Si può immaginare come un piano di vetro posto davanti all'oggetto, sul quale i raggi proiettanti paralleli che individuano il contorno dell'oggetto tracciano l'immagine assonometrica.
La direzione dei raggi proiettanti può essere obliqua oppure ortogonale al quadro II. Di conseguenza l'assonometria si distingue in ortogonale e obliqua. Le assonometrie oblique sono le assonometrie in cui i raggi proiettanti, paralleli fra loro, risultano inclinati rispetto al piano assonometrico o quadro. Fanno parte di questo tipo di assonometrie:
- l'assonometria cavaliera isometrica;
- l'assonometria cavaliera dimetrica;
- l'assonometria cavaliera militare.
Nell'assonometria ortogonale gli assi x,'y, z proiettati sul quadro in x', y', z' si presentano con angoli variabili fra loro in relazione all'inclinazione del quadro rispetto ai piani.. Fanno parte di questo tipo di assonometrie:
- l'assonometria isometrica;
- l'assonometria dimetrica;
- l'assonometria trimetrica.

Assonometrie oblique.
1)Assonometria cavaliera isometrica.
È così chiamata perché le dimensioni lineari, parallele ai tre assi, non variano rispetto a quelle del disegno di riferimento in proiezioni ortogonali. Nell'assonometria cavaliera isometrica il quadro assonometrico è disposto in genere coincidente o parallelo al piano orizzontale: in questo caso i raggi proiettanti obliqui traslano le facce orizzontali di un solido (per esempio un cubo) mantenendo invariate sia le dimensioni dei lati sia quelle dei loro angoli. In questo tipo di assonometria si è stabilito, per convenzione, che gli assi x e y formino fra loro un angolo di 90°, mentre l'asse z forma con gli altri due un angolo di 135°. In pratica però, per evitare l'inconveniente della sovrapposizione degli spigoli verticali dei solidi a base quadrata e delle loro diagonali, si preferisce ruotare gli assi x e y in modo da formare con l'orizzontale angoli di 30° e 60° e con l'asse z angoli di 120° e 150°).
2)Assonometria cavaliera dimetrica.
In questo tipo di assonometria il quadro assonometrico è parallelo o coincide con il piano verticale, di conseguenza gli assi x e z formano fra loro un angolo di 90°; poiché il prospetto non muta le proprie dimensioni, anche le misure sui due assi rimangono invariate. Per un tracciamento immediato dell'assonometria si è stabilito, per convenzione, che il terzo asse y, corrispondente alla linea della profondità, sia inclinato di 45° rispetto a uno degli altri due e di riportare su di questo le misure dimezzate al fine di ottenere una miglior resa visiva. 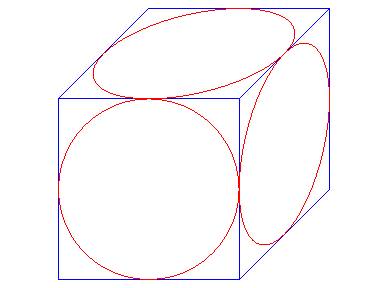Per rappresentare in assonometria cavaliera dimetrica una circonferenza o parti di questa, occorre utilizzare una figura ausiliaria collocata in genere tangente all'asse di riferimento (orizzontale per figure piane orizzontali, verticale per figure piane verticali): la circonferenza va inserita in un quadrato; tracciando gli assi e le diagonali del quadrato, si individuano sulla circonferenza otto punti che, riportati nella corrispettiva figura ausiliaria in assonometria, permettono, con l'uso di curvilinee, di tracciare la circonferenza.
3)Assonometria cavaliera militare.
Questo tipo di assonometria fu usato soprattutto in Francia nel XVI sec. dagli ingegneri militari che la utilizzano per i disegni delle fortificazioni poste sopra le trincee. L’assonometria cavaliera militare viene detta anche rapida, appunto per la rapidità di esecuzione. Facciamo coincidere il quadro II col P.O. In questo modo coincidiamo Q e il quadro di proiezione sono gli assi x e y, i quali rimangono perchè sono perpendicolari fra loro cioè formano un angolo di 90°. Ad essere proiettata veramente sul P.O: è invece l'asse z Mentre su x e y si riportano le misure effettive, le misure su z possono allungarsi o scorciarsi o rimanere invariate in rapporto all'inclinazione del raggio proiettante r. Nella pratica del disegno, poiché z è l'asse delle altezze, l'effetto visivo peggiora se si allungano e soprattutto se si accorciano le altezze, per cui conviene riportare le misure effettive anche su z. In questo tipo di assonometria conviene avere l'asse z in posizione verticale, cioè perpendicolare ad una orizzontale di appoggio che serve anche come base di partenza per l'esecuzione del disegno. Per non far coincidere l'asse z con uno degli altri due, occorre però disporre l'angolo retto formato da x e y in modo che sia inclinato con questa linea di base. Generalmente si inclina uno dei due assi di 30° e l'altro di 60°. È indifferente quale dei due debba essere inclinato di 30° e quale di 60° e la scelta sarà dettata soltanto da opportunità di disegno. Una scelta di due angoli di 45°, pur non essendo sbagliata, è sconsigliabile perché può creare ambiguità di visione. Sistemati gli assi l'esecuzione, è poi semplice e rapida perché basta riportare, tale e quale com'è, la pianta dalle proiezioni ortogonali all'assonometria collocandola sugli assi x e y e, dai vertici della pianta così riportata, innalzare le altezze parallelamente a z.

Assonometria ortogonale.
1) Assonometria isometrica
Assonometria isometrica (una sola scala di riduzione) Nella pratica del disegno scegliamo i tre punti A,B,C equidistanti da O; il triangolo fondamentale è un triangolo equilatero e quindi TT ha la stessa inclinazione rispetto ai tre piani cartesiani. In questo caso gli angoli tra gli assi so.no tutti uguali tra loro (120°, 120°, 120°). L'unità di misura riportata su qualunque dei tre assi subisce un uguale rapporto di riduzione. Per questo l'assonometria viene detta isometrica (stessa misura).
2)Assonometria dimetrica.
I tre angoli formati dalla proiezione degli assi sul quadro sono due uguali e uno disuguale. Basterà assolvere a questa condizione per poter disegnare l'assonometria. L'unità di misura in questo caso subirà lo stesso rapporto di riduzione sui due assi che delimitano l'angolo differente (in figura z e y), e un diverso rapporto di riduzione sul restante asse (x).
4)Assonometria Trimetrica.
L’assonometria trimetrica si ha quando il quadro II è diversamente inclinato rispetto a tutti e tre i piani cartesiani di riferimento; gli angoli fra gli assi sono tutti disuguali e le unità assonometriche si ridurranno in tre modi diversi.