PROIEZIONI ORTOGONALI.

Le proiezioni ortogonali rappresentano uno dei tanti metodi propri della geometria descrittiva per rappresentare oggetti, di forma qualunque, mediante un disegno. La geometria Euclidea comprende l'insieme delle teorie matematiche alla base delle relazioni tra gli enti fondamentali della geometria: punto, retta e piano. La geometria descrittiva tratta invece le relazioni fondamentali che legano le proiezioni degli enti fondamentali della geometria Euclidea: proiezioni di punti, di rette, di piani , dello spazio che si vuole rappresentare sul foglio da disegno; relazioni fondamentali sono l'appartenenza, il parallelismo, la perpendicolarità ecc... La geometria descrittiva ha per scopo proprio lo studio dei diversi metodi con i quali si possono rappresentare, mediante un disegno, oggetti a tre dimensioni su un unico piano, quello del foglio. Di metodi di rappresentazione se ne possono immaginare infiniti, ma il metodo dovuto a Gaspard Monge, o delle proiezioni ortogonali, è quello che il disegno tecnico ha fatto proprio. La carta geografica è un esempio di proiezione su un piano di una superficie curva con proporzioni alterate. Anche la superficie terrestre viene rappresentata con metodi di proiezione ma, poiché la superficie della terra è curva, le reali dimensioni dei continenti sono deformate in modo più o meno marcato quando essi sono rappresentati su un solo piano. 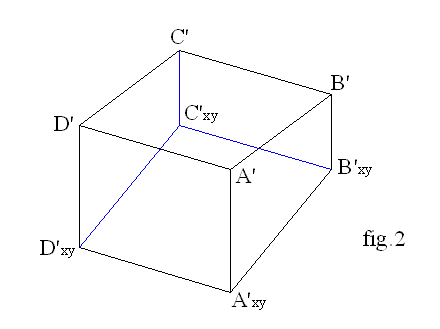Si definisce proiezione ortogonale di un punto P su un piano p-greco , il punto P1, intersezione tra la retta perpendicolare condotta per P e il piano p-greco. La proiezione ortogonale di una qualunque figura, piana o solida, è la proiezione ortogonale di tutti i punti che la compongono.Se la figura è parallela al piano di proiezione, la sua proiezione è identica alla figura stessa. Se la figura è inclinata rispetto al piano di proiezione, la sua proiezione è deformata. Anche la proiezione ortogonale di una figura solida è la proiezione di tutti i punti che la compongono. Per costruire tale proiezione è sufficiente proiettare solo quei vertici e quegli spigoli incontrati dai raggi proiettanti nel loro percorso verso il piano di proiezione. Infatti gli spigoli "in ombra" rispetto ai raggi proiettanti, hanno proiezioni interne o al più coincidenti rispetto agli spigoli che impediscono loro di essere "colpiti direttamente" dai raggi proiettanti La proiezione ortogonale di una figura solida coincide quindi con l’ombra della figura generata da raggi solari perpendicolari (ortogonali) al piano di proiezione. Il metodo delle proiezioni ortogonali (o di Monge) ha lo scopo di rappresentare sul piano (il foglio da disegno) figure geometriche qualsiasi e comunque disposte nello spazio. Per rappresentare completamente una figura geometrica nello spazio, questo metodo impiega tre piani fondamentali di proiezione perpendicolari tra loro. Per individuarli nella realtà, basta guardare l'angolo in basso a destra della stanza in cui ci troviamo: il piano dei pavimento, il piano della parete di fronte a noi e il piano della parete alla nostra destra corrispondono ai tre piani di proiezione Le intersezioni di questi tre piani (delle pareti) rappresentano la terna di assi cartesiani x, y e z di riferimento per le coordinate degli oggetti da rappresentare. Le proiezioni ortogonali di un oggetto sui tre piani ortogonali del metodo di Monge corrispondono alle proiezioni ortogonali dell'oggetto, immaginato all'interno della stanza e proiettato sui piani del pavimento, della parete di fronte a noi e della parete alla nostra destra. Ai tre piani fondamentali di proiezione si usa ancora dare il nome di piano orizzontale (PO), piano verticale (PV) e piano laterale (PL). Più propriamente i piani sono identificati dagli assi che li definiscono:
-Il piano orizzontale (PO) = piano xy;
-Il piano verticale (PV) = piano xz;
-Il piano laterale (PL) = piano yz.
Per poter rappresentare sull'unico piano dei foglio da disegno questi tre piani perpendicolari tra loro e disposti quindi nello spazio, si ricorre al seguente artificio:
1) si fa coincidere il piano verticale con il piano del foglio da disegno;
2) si ruota il piano laterale intorno all'asse z di 90' ribaltandolo sul PV;
3) si ruota il piano orizzontale intorno all'asse x di 90° ribaltando così anch'esso sul PV.
Ora i tre piani giacciono tutti sul piano dei foglio da disegno, ma ciascuno conterrà una proiezione diversa della figura geometrica che si vuoi rappresentare. La proiezione ortogonale sul piano xy (PO) prende il nome di vista dall'alto (o prima proiezione o pianta), quella sul piano xz (PV) di vista di fronte (o seconda proiezione o prospetto), quella sul piano yz (PL) di vista da sinistra (o terza proiezione o profilo). La posizione degli assi x, y e z, che a prima vista può sembrare un po' inconsueta, è dovuta alla necessaria rotazione nello spazio della terna di assi destrorsa che in tal modo può adattarsi al metodo delle proiezioni ortogonali.